There's no way around it - math is a key part of the management consulting selection process. You are going to need to prep your math if you want to have a chance of landing any consulting job, let alone at a top-flight role at an MBB or similar firm.
Even before you make it to case interviews, the latest aptitude tests and online cases being rolled out by the major consulting firms are featuring more and more mathematical questions. Particularly prominent examples are BCG's Casey chatbot case study and the new versions of McKinsey's Solve assessment - both have substantial, demanding math components.
If and when you make it through to case interviews, these will almost certainly feature another wall of math for you to make it through - and you will have to work hard to impress your interviewer here, as expectations will be high. This is somewhere where far too many candidates fail to prepare properly and really let themselves down.
Now, this might seem contradictory, but, whilst your math needs to be very sharp to land a consulting job, you simultaneously won't need a huge depth of mathematical knowledge to do well. You certainly don't need to come from a quantitative background at university - indeed, the math you were doing by age 16 in high school will be more than sufficient.
However,the key thing to note is that consulting math is very different to academic math. Even if you do have strong mathematcial training, you won't get far approaching problems the same way you did at university.
In this article, we'll first look at what makes math so important for aspiring consultants and what makes consulting math different. We'll then run through the areas in which you need to be proficient, whilst giving some tips on "hacks" that you can use to excel in tests and interviews.
Math is one of the most important elements of preparing for a consulting interview, and this article is a great point of entry into the subject. However, it is impossible to be fully comprehensive in any reasonable amount of space - for a start, we're not going to reproduce your high school math textbook here!
Where appropriate, we'll point you towards useful public resources, including other articles on this site. Generally, though, if you want a more comprehensive source, you should check out the full Consulting math content within our comprehensive Case Academy course:
If you want to start off with just that math content, you can find this in isolation in our Consulting Math package:
Finally, if consulting prep rightly seems daunting to do alone, you can investigate getting some coaching from real consultants here:
This article will get you started, but the these additional sources will give everything you need to have a real chance at landing your dream consulting job!
Consulting math in principle
You might think that “math is math” and that being good at academic math - perhaps at a university level - will mean you have nothing to fear from a consulting interview conducted at a high school level. Certainly, being good at math in an academic context is a solid advantage going into a consulting interview. However, the style of math used in consulting is very different from that used in academia, and takes practice to pick up. Even a very accomplished mathematician will struggle to impress if they don't approach problems in the way their interviewer expects.
In academic math, the overriding concern is accuracy. It might take a lot of complex work and a great deal of time to get there, but what matters is that the answer is absolutely watertight. Consulting math is a very different beast. Working consultants - and consulting interview candidates - are always under heavy time pressure. Results are what matter and answers are required simply to be good enough to guide business decisions, rather than being absolutely correct.
A 90% accurate answer now is a lot more useful than a 100% accurate one after a week of in-depth analysis. The additional mathematical complexity required to reach such a totally accurate, precise answer is simply not required. Instead, consultants will simplify their analyses to be more time efficient.
In case interviews, special importance will be ascribed to mental math. Of course, being able to do mental math quickly demonstrates mental agility. However, consultants also frequently use quick mental math to impress clients (and thus help justify their fees). The sharper your mental math, the more impressed your interviewer will be. We include a brief section on mental math skills below, with much more detailed treatment in the MCC Academy or our specific math package.
Consulting math in practice

Now we know a little about how academic and consulting math differ. This is good knowledge to have, but we should keep an eye on practicalities of how things will actually be in the consulting selection process. Let's get some of the most straightforward matters out of the way before we look at consulting math in more depth.
In this article, we'll primarily focus on math for case interview, just as that's the tougher nut to crack. Math for tests or online cases will generally be at the same conceptual level, but with calculators and/or Excel allowed and without having to constantly explain your reasoning to a harsh audience.
That said, the math for tests and online cases is certainly not easy, and we include some specific notes on prepping for these throughout this article.
Case Interview Specifics
Perform Calculations on Paper
In case interviews, you will be given a piece of paper and should feel free to use it when doing calculations.
Don't Rush
The time pressure in case interviews is severe, and you cannot afford to waste a second. By the same token, though, taking a few extra seconds to get to a correct answer is always preferable to producing an incorrect answer a few seconds more quickly. Don't be afraid to take the time you need. "Slow is smooth and smooth is fast".
Be Assertive
Candidates who are not really comfortable with math tend to state their answers as questions - with a rise in vocal pitch towards the end of the sentence. Interviewers will notice this and take note. Successful candidates will sound confident and state their answers with an air of certainty.
Ask About Rounding
Ask your interviewer if it's okay to round numbers in your calculations. Generally, they will be fine with this, and you may do so.
Math for Aptitude Tests and Online Cases
We'll include some specific notes on math for screening tests and/or online cases as we go. Online cases in particular are increasingly being deployed either before or alongside first round case interviews and have been featuring more and more math.
In general, though, the kind of math, and the conceptual level it's pitched at, will remain the same as for case interviews. Nothing will be more complicated than basic high school math, with the focus still very much falling on things like percentages, charts, multiplication etc.
As we note in the relevant section in this article, one very small change has been a move away from "average" simply being synonymous with "mean". Instead, newer tests are increasingly asking candidates to calculate median and modal values as well.
However, the really salient difference between case interview math and that found in aptitude tests, online cases and the like is that the latter allow you to use calculators and/or Excel. This doesn't necessarily make things easier so much as change the emphasis of math questions quite a bit.
In case interviews, big part of the challenge is simply performing the calculations sufficiently quickly - with this entailing clever use of estimation/approximation to deal with large numbers in timely fashion. By contrast, with access to electronic help in online tests and cases, arithmetic becomes trivially easy and approximations become unnecessary.
Now, the emphasis is on how you set up calculations and figure out how to get to the answer you need. For sure, this is very important in case interviews as well, but the presence of calculators etc allows this aspect of the math to be made more demanding. Thus, you can expect to have to use a little more algebra and/or conduct more multi-step calculations. You will also be given less time to complete questions, in light of the fact you have help.
In terms of preparation, things stay very largely the same, and all the case interview focused material from this article will carry over directly.
The main thing to add is to spend some time solving problems with a calculator and/or Excel - especially if you don't do this day-to-day. If you aren't proficient with Excel already and don't have long until your test/online case, don't worry and stick to calculator practice. However, if you have a little more time and/or a little more starting proficiency, getting up to speed can provide a small, but real, advantage in certain questions - particularly where you need to calculate averages.
Forget outdated, framework-based guides...
Interviewers are sick of seeing candidates miss the point and make the same old mistakes. Stand out from the crowd by learning to think like a working consultant! Get startedFundamentals: a checklist of consulting math skills
So, which math skills do you need?
Here, we'll go through the main areas you should cover to prep for a standard MBB interview or aptitude test/online case.
We go into much more depth on each issue - along with worked examples and "hacks" for quicker calculations - in our video lesson in the MCC Academy and our math package.
Of course, though, if you really weren't paying any attention in school and are totally in the dark as to what a fraction is - there is a point where you will simply need to pick up a basic math textbook or fire up Google.
1. Fractions
Fractions are a convenient way to represent numbers between 0 and 1 as parts of a whole. For instance, we might write 0.5 as 1 / 2 (or simply 1/2). For case interviews, you should be readily able to add/subtract and multiply/divide fractions. There are a couple of ways to manipulate fractions that will be particularly useful:
Approximating Divisions
Say you have to work out 107 ÷ 13. You only have a few seconds and no calculator. You definitely don't have time for long division - so what will you do? The interviewer is waiting...
One great use of fractions is allowing you to tackle complex divisions quickly. For example, let's imagine we do indeed have to divide 107 by 13:
We know that:

Thus:

This method gives us a good-enough answer to proceed with our analysis, with only a few seconds work and no need for a calculator. Success!
Efficiently Navigating Math Problems
Fractions also help simplify your analysis of certain problems. Let's take a relatively simple example:
1/3 of a company's employees are software engineers. Due to new generative AI tools increasing productivity, 1/3 of the software engineers are to be laid off. What fraction of the remaining employees are software engineers?
Software engineers laid off:

Remaining software engineers:

Employees remaining in the company:

Therefore, the fraction of remaining employees who are software engineers is:

2. Ratios
Ratios are close cousins of fractions and tell us how much of one thing we have in relation to another.
For instance, if we have three pens, four pencils, and one eraser, then the ratio between them is 3:4:1.
Join thousands of other candidates cracking cases like pros
At MyConsultingCoach we teach you how to solve cases like a consultant Get startedFractions come up in all kinds of business problems. For solving case studies, it is often very useful to express ratios as fractions of the whole.
For example, we can re-express the ratio between our items of stationery above as 3 / 8 : 4 / 8 : 1 / 8 . This then allows you to address problems using a similar method to how we solved our example of software engineers exiting a workforce, above.
Think about how you might address the following question:
Restaurant Barbello’s profits are split among food, drinks and tips in a 7:3:2 ratio. If the profit for food is $360 more than that for drinks, what is the total profit?
You should be able to arrive at an answer very quickly - certainly in under a minute. We show you how to do so in a MCC Academy, also available in our specific math package.
3. Percentages
Similar to fractions and ratios, we can think of percentages as ratios where one number is fixed at 100, or as fractions where the denominator is always 100.
Percentages are as ubiquitous in the business world as they are in interview case studies and online tests and cases. Indeed, the most recent online cases - particularly newer versions of the McKinsey Solve assessment - have asked candidates to make a lot of percentage calculations, especially percentage changes in quantities.
In case studies, we might be dealing with profits that are down 40%, targeting increases in sales or revenue by 20% or attempting to cut costs by 15%. We are especially likely to deal with percentages when addressing issues around pricing - such as applying mark-ups on products to generate profit or offering discounts to promote sales.
Note that percentages will sometimes be discussed in terms of "percentage points". As such, if you are told that revenues are down by 20 percentage points - or even just 20 points - this simply means that revenues have fallen by 20%.
You can test your ability to work with percentages by seeing how quickly you can figure out an answer to the following:
Marta has a shop selling handbags for €30. She offers a 20% discount for one day. She then realises that the price is now too low, so she increases the price by 10%. What it is the current price of Marta's Handbags?
In the MCC Academy math video, also included in our specific math package we show how to answer this question in just a few seconds.
4. Probability
Nothing is certain in the business world. Thus, when consultants make decisions, they must constantly evaluate the probabilities of different future events.
The probability of such an event will always be a number between 0 (impossible) and 1 (certain), calculated as the number of ways that an event can happen, divided by the total number of possible outcomes. Therefore, the probability of rolling a six on a fair die is 1/6, as there are a total of six possible outcomes, only one of which is the event in question.
The probability of an event not happening is 1 minus the probability that it will occur. In proper notation, this is:

You also need to know how to calculate the probability of multiple chance events all occurring. Luckily, in case interviews, tests etc, you will only have to deal with independent events, where individual outcomes do not influence subsequent ones.
The standard example here is coin tosses, where the probability of heads on each new toss remains 0.5, regardless of the results of previous tosses (despite any intuitions in line with the gambler's fallacy). This is as opposed to dependent events, where the outcomes of one event can influence subsequent ones. You might recall examples of these events from school problems about taking coloured balls out of vases without replacing them - in any case, we don't need to worry about dependent events here!
The probability of multiple independent events all happening is calculated simply as the product of their individual probabilities. To illustrate, the probability of heads (P(H)) on the toss of a fair coin is 0.5. Therefore, the probability of tossing heads three times in a row is:

Expected Returns
Probability is especially relevant to business where we need to calculate expected returns. Here, we weight the yield promised by an investment by the probability that it will pay off. This then acts as a guide to decisions about which investment opportunities should be pursued.
Say we have $100 to invest and that we can choose between two opportunities that will pay out after one year. Option A will pay out $120 with a probability of 0.9, whereas option B promises to pay out $150, but with a probability of only 0.7.
The expected returns are:
| Option A: | 0.9 x 120 = $108 |
| Option B: | 0.7 x 150 = $105 |
As such, we should favour option A as yielding a greater expected return, despite option B's greater headline payout.
This is a very simple example. However, we take a look how to calculate a more complex expected return in the MCC Academy video lesson, also available in our consulting math package.
5. Averages
We can think of an average as a measure of the "typical" value of some series of numbers.
Unless you are told otherwise, any talk of averages in a case interview will refer specifically to the mean (very specifically the arithmetic if you want to be nerdy about it...). This is calculated as the sum of all the numbers in the series, divided by the number of those numbers.
We can state this more formally as:

Means are fairly straightforward. The only complexities you will need to worry about arise when the values you are averaging do not have the same weight as one another. In such cases, the calculations will start to look rather like those for expected returns, where appropriate weightings are applied.
Let's take an example to see how well you can manipulate means. How long does it take you to solve this problem? Could you do so under time pressure in a case interview?
A company has 80 employees. 25% work on average 6 hours a day, 65% work 8 hours and the rest 12 hours a day. What is the average time for which an employee works?
We show you two different ways to solve this problem in the MCC Academy math material.
Now, whilst averages are typically synonymous with means in case interviews, there has been a little more variation in kinds of average coming up amongst the recent proliferation of online cases as part of the consulting selection process. Specifically, questions have frequently been asking candidates to calculate the mode and/or median of datasets.
These averages can be a little more tricky to manually compute than the mean - not more difficult so much as more time consuming and annoying. Luckily, these online cases allow for calculators and/or Excel to make things more straigtforward. Thus, it's definitely worth getting good at using these to find the mean, mode and median before you sit tests like McKinsey's Solve or BCG's Casey
6. Rates
Rates are ubiquitous across the business world in general and within consulting in particular. We can think about rates as a ratio or fraction where the denominator is always 1. Some rates you will encounter include the interest rate, the rate of inflation, various tax rates, the rate of return on an investment and the exchange rates between currencies.
Rates are very common in case studies and will generally be expressed per year or per annum. Candidates can easily become confused, though, where information is not all provided in the same units. As such, it is best to convert all such quantities into one single set of units to facilitate comparison. For example, with a mix of monthly and annual rates, it might be best (depending on the details of the problem) to convert all the relevant figures into per annum rates.
In the MCC Academy math lesson, we work through a business case study, advising a firm whether to invest in new equipment, based on an analysis of different rates. This demonstrates how central rates can be to business problems, as well as how to work with them efficiently.
7. Optimisation
A lot of business problems will boil down to the optimisation of one or more salient variables. Optimisation in a mathematical context can be a mind-bendingly complex affair. Indeed, optimisation of complex, non-linear problems is a substantial area of academic study, with real-world applications ranging from engineering to finance.
Mercifully, though, optimisation in consulting interviews and tests is a pretty straightforward affair. The business problems you are given will almost invariably be linear. That is, their form will resemble something like y = ax + b.
This means that the relevant variable will be optimised at one of the function's boundaries. To establish which boundary value yields the optimum, we simply need to work out the gradient of the function - or, more simply, whether this gradient is positive or negative.
As such, if we are trying to maximise y for the function below, where y = 2x + 1, between x=0 and x=4, we can see that the positive gradient (upward slope) of the line means that y will be maximised for the maximum possible value of x - which is 4 in this instance.
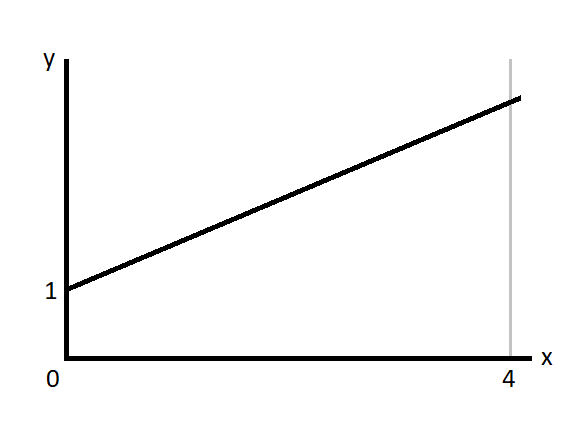
Note that, in the section on writing equations below, we also discuss a way to solve these kinds of linear optimisation problems without doing any calculations or referring to a graph.
For now, let's try an example of the kind of optimisation that you might have to deal with in a case interview:
Your client is Ginetto’s gelato, a shop that sells ice cream in London. They make fresh ice cream on-site every day using high quality, organic ingredients. If they have excess ice cream, they freeze it to make ice lollies that are then sold to another retailer. Making a kilo of ice cream costs Ginetto £15, and it is sold for £30. Ice lollies, however, can only be sold for £12. On any given day, the shop expects to sell 100kg of ice cream if it is sunny and only 30kg if it is rainy. In London, the probability of rain on any given day is 75%. Ginetto has asked you how much gelato they should make to maximize their profit.
This will seem pretty difficult if you don't know what you're doing. However, in the MCC Academy and our math package, we show you how to optimise Ginetto's ice cream production in two different ways, demonstrating how to deal with these kinds of case questions in straightforward and - crucially - time efficient fashion.
Charts

The article up to here pretty much covers the fundamental math you will need for case interviews and/or aptitude tests. However, there are other, related skills that you will need, beyond familiarity with these basic concepts.
Some mathematical skills will be required throughout the case, not just in computing final solutions. In particular, it is likely that you will have to interpret charts as you work through your analysis.
Case interviews are not like exams, where you simply receive a question and solve it without further input. Rather, there is an ongoing dialogue between the interviewer and the candidate. Generally, you will need to acquire more and more information in order to eventually answer the interviewer's main question. This will often be provided to you in the form of charts - meaning that you will have to be able to interpret these charts in order to get the information you need.
Looking for an all-inclusive, peace of mind program?
Choose our mentoring programs to get access to all our resources, a customised study plan and a dedicated experienced MBB mentor Learn moreChart Basics
As a starting point, you should be familiar with the kind of basic graphs and tables you might recognise from Excel. As well as standard tables of values, you should be entirely comfortable reading the following:
Charts in Online Cases and Aptitude Tests
Most of the time, the role of charts in aptitude tests and/or online cases will be very much the same as that in traditional case interviews. That is, you will be presented with charts to interpret so as to provide information to answer questions.
However, recent versions of the McKinsey Solve assessment in particular have turned things on their head and asked candidates to create charts to best express information.
Rather than start from scratch with something like Excel, though, test-takers have been asked to decide a few variables, such as the particular data set/s to be represented and the kind of chart to use - pie, line, scatter, bar or other. The test's software then does the work of actually generating the final chart.
Candidates we have spoken to have often regarded the choice of chart type as the most difficult aspect of this question, which leads neatly into our next section...
Charts at Higher Level
Even these basic kinds of charts can take multiple forms, though, and it can be a more useful distinction to categorise charts by their function in conveying information, rather than their specific form. As such, we can think about these charts as records of the following:
Comparisons/Relationships - showing a correlation or pattern - generally with a bar or line graph. For example, demand for a product versus the age of buyers.
Distributions - showing how data is distributed to provide the viewer with a sense of the mean, standard deviation, etc., generally with pie or bar charts. For example, the bodyweights of a group of individuals.
Trends - quantities are shown over a period of time, so as to identify seasonal variations, generally with a line graph. For example, weekly sales of a product over a three year period.
Composition - showing how a whole is divided into parts, generally with a pie chart or scatter plot. For example, the market share of different car producers in a geographic region.
Adding Complexity to Charts
The charts you have to interpret in case interviews and online tests will often be rather more complex than a basic pie chart or bar graph. Charts become more complex as more and more information is added to them - generally by allowing data to be encoded in additional dimensions.
Given there are an indefinite number of ways for this to be done, it is impossible to give an exhaustive treatment here (though we discuss case study charts in more detail in MCC Academy and our math package). Indeed, as charts become more complex, they are often merged with graphic design elements, and there is an increasing trend in the business world towards producing fully-fledged infographics.
Example: Stacked bar charts
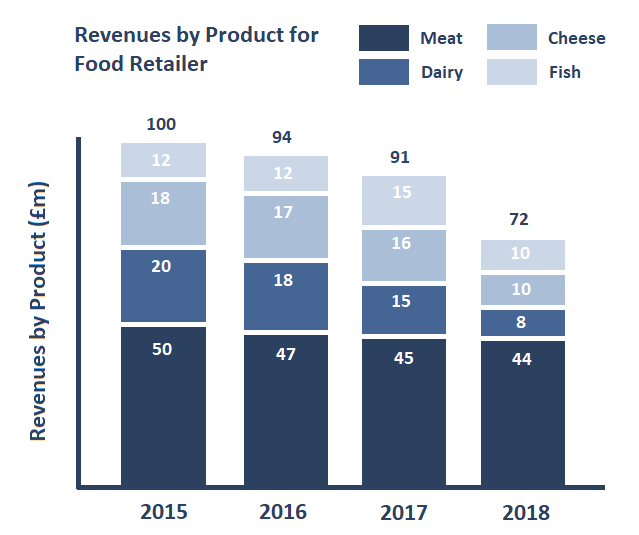
To take what is still a relatively simple example, we can significantly increase information content by generating "stacked" bar charts, where each bar is subdivided into constituent portions. Often, even more data will be added by recording additional values against each bar.
Below, we can see how a stacked bar chart provides information about the specific product breakdown accounting for a food retailer's overall annual revenues:
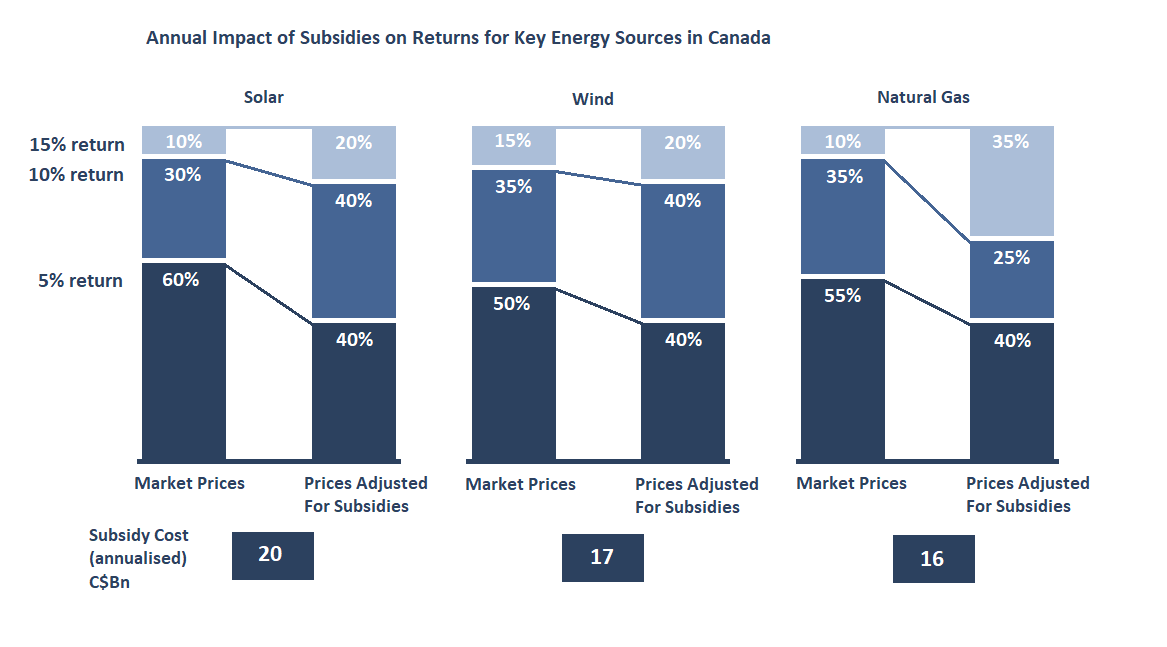
Stacked bar charts can be used to provide information about the relationships between quantities. For example, the chart below shows the effect of government subsidies on the returns generated by different energy sources in Canada:
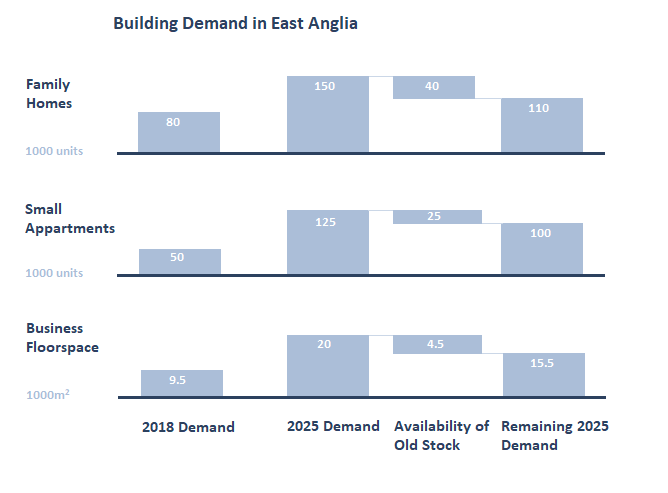
Alternatively, stacked bar charts can also be used to show the differences between quantities. Below, we see data showing changing demand for various types of building in a region of England. The chart allows us to appreciate the rising demand for buildings as well as the extent to which this might be ameliorated by existing buildings re-entering the market.
Example: Complex Tables
Case studies will very often contain complex tables, displaying information in multiple dimensions. You will need to quickly interpret these and pull out key values.
An example is shown below. Here, we see the success of a large, multi-channel advertising campaign, made by a new political party in order to secure public donations.
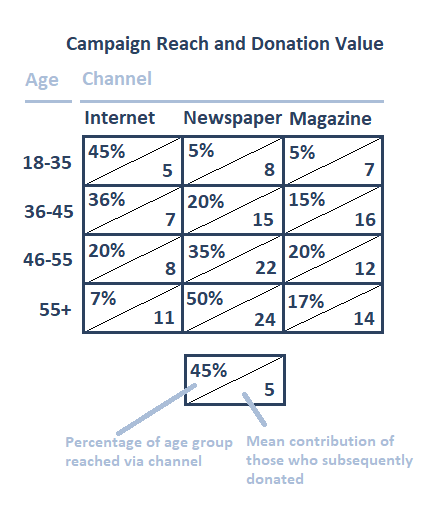
We discuss these complex tables in more detail in a lesson in the MCC Academy, also included in our separate math package.
Writing equations
In simpler case studies, you will be able to analyse scenarios verbally and move straight to the relevant arithmetic without having to resort to equations. However, as cases become more complex, this becomes exponentially more difficult. Soon, it becomes impossible to keep track of all the variables and all the relationships between them.
In such cases, you should be able to express the problem as an equation. This will allow you to engage in more complex reasoning and keep track of more items than you can hope to verbally.
Let's look at an example of how we have to adapt as problems become more complex:
Q1: I am 25 years old and my sister is 3 years older than me. What is my sister’s age?
This problem is easy to solve with basic arithmetic. Thus, the sister's age is simply 25+3=28yrs.
Q2: I am 25 years old today. 5 years before I was born, my father’s age was 19 years less than double my age 5 years ago. What is my father’s age today?
Now it is much harder to solve the problem directly as before. However, an equation makes
matters easy. If we make our own age the variable


Being comfortable with equations has other benefits too. In the simple, linear optimisations we looked at above, having the relevant equation and knowing the boundary conditions is enough to be able to optimise the function.
In the straightforward example we looked at, if we are trying to maximise y = 2x + 1 for x between 0 and 4, then the fact that the coefficient of x (that is, 2) here is positive is enough for us to know that the graph will have an upward slope. Thus, the function will be maximised at the upper bound of x - which will be x = 4 in this case. Thus, we have an answer without drawing a graph or doing any calculations!
Mental math "hacks", tricks and timesavers
As we noted at the start of this article, consultants take mental math very seriously and you will need your calculations to be sharp in interview if you want to get a job. We have already noted a few "hacks" that will help you perform some operations more quickly. However, these are just a small subset of a whole host of such skills which you should be able to draw upon.
Our video lesson on consulting math in MCC Academy and our math package covers a full set of these skills. Here, though, we'll just take a look at a couple of these techniques to get an idea of the kind of methods consultants use day-to-day to make quick calculations - and that are invaluable in case interviews.
X% of Y is Y% of X
What is 28% of 75? Difficult, isn't it?
Well, not really. The answer will be the same as 75% of 28, which is much easier to calculate. Since we should already know that 28 ÷ 4 = 7, 75% of 28 is just 3 x 7 = 21. Easy!
Rule of 11
63 x 11 = what?
If you have to think about this for more than two seconds, you are too slow.
Luckily, there is a rule here that can help. Specifically, if you have to multiply a two-digit number by 11, you simply add the two digits together and place whatever the result is between them.
As such, for 63 x 11, we add 6 + 3 = 9 and put that 9 between 6 and 3 to get 693 - the correct answer! Similarly, if we wanted to multiply 26 by 11, we would add 2 + 6 = 8, giving an answer of 286.
If you want to learn similar techniques to be able to almost instantly calculate that 4900 ÷ 50 = 98, or that 387 ÷ 9 is 43, then you should check out the math content in our MCC Academy or our consulting math package.
It's tempting to think of these kinds of "tricks" as "optional extras" in your case interview prep. However, you must remember what we said earlier about consulting math being an entirely different beast versus the academic math to which you are accustomed. In this context, these kinds of quick calculation methods are core skills. Indeed, you can expect to need these skills to impress your interviewer enough to land an MBB or any top-tier consulting job.
To make sure your mental math is as sharp as it possibly can be, you should be practicing constantly, right up until your interview. You will get some work in during case practice (remember to check out our free case bank), but you should also be practicing math separately.
Our free mental math tool is a great resource here, as is our specialist math package:
- Video Lecture on Foundations of consulting math
- Video Lecture on Applied consulting math
- Video Lecture on Advanced topics in consulting math
- Video lecture on Advanced methods in mental math
- Actionable advice on how to improve your calculation speed and accuracy
- 60+ chart based questions with detailed solutions
- 100+ business problems with detailed solutions
- Mental math tool to improve mental calculations speed
Takeaway
This article gives you a great idea of the math you need to cover as you prep for your case interviews and/or any aptitude tests or online cases. It might be a relief for some of you to find out that the mathematical concepts required are not hugely complex. However, it's crucial not to become complacent as a result!
The challenge is not in the level of the math itself, but in being able to conduct the relevant calculations efficiently and very quickly. In interviews, this will be without the help of a calculator or computer and with your interviewer impatiently bearing down on you.
Now that you know which mathematical topics you need to get up to speed on, you should get the basics firmly established in your mind and immediately move strait to practice. Our free mental math tool is a great resource here, as is our math package.
Mental math in particular is a skill in itself, though, and there are specific techniques or "hacks" that you should learn if you want to impress in case interviews. The content in this article is a great start, though the most comprehensive resource remains our material on the subject in the MCC Academy also included in the aforementioned math package. This takes a detailed look at a whole range of techniques to massively speed up your calculations.