McKinsey PST: an adaptive learning approach to pass the test
The McKinsey Problem Solving Test (McKinsey PST) is a data interpretation and critical number reasoning test used by McKinsey to select candidates to be admitted to the first round of case interviews. The use of the PST is the main difference between the McKinsey recruiting process and those of its main competitors. The other distinct element is the PEI, or Personal Experience Interview. However, with this set of questions on personal impact McKinsey closely approximates the fit interviews of other firms.
The McKinsey PST is so notoriously difficult because it tests a very diverse skillset and requires you to work under the tightest of time constraints. Of those candidates good enough to be considered and given the PST McKinsey only pass one in three - where failure means immediate rejection. However, we are proud to say that despite the average PST pass rate being so low, 85% of candidates who use our course pass their own PST. For anyone who doesn't pass, we return half of their money.
This article serves as a guide to help you prepare for your McKinsey PST. We begin with an overview of what the PST is all about - this gives you a five minute briefing on all the essential information and the context of the PST.
Next, we spend some time going through each kind of PST question in turn, providing structured approaches to tackling them, complete with fully-worked PST example questions and specific PST tips and tricks which might come in useful.
Finally, we put everything together, with step-by-step guidelines on how to prepare for McKinsey PST success using our adaptive learning methodology.
Practice tests developed by McKinsey consultants
Learn morePST Basics
There are seven key facts which you will need to know about the McKinsey PST:
1. Who Has to Do the PST?
Not everyone has to do the McKinsey Problem Solving Test. Experienced hires and those recruited from top-tier business schools are often spared. However, in general, anyone applying to an entry-level business analyst role will be expected to pass the McKinsey PST to be considered.
If you are not sure whether you will be required to do the PST, your default assumption should be that you will, but you should ask with the HR team at the office you are applying to so as to be certain - this is a perfectly reasonable enquiry to make.
2. Format: 26 Questions, Pen and Paper
The PST is a multiple choice test completed on paper. 26 questions are divided between three business cases. These cases test how you would perform in the different phases of a consulting project: client interaction, problem definition, problem solving, analytical work and implementation. The cases are on the kinds of issues that real consultants will encounter in the field, including problems on market entry, profitability and operational improvement.
3. 60 Minutes
Quite simply, if you had three hours to work on an individual McKinsey PST, you could pass easily without any help. Time is the single major constraint in the PST. You are not allowed to use a calculator, computer or any other time saving device beyond your own brain, you need to make sure you have developed and practiced the required skillset - especially time saving skills - and approach the test as a whole with the most effective possible strategy.
60 minutes equates to just over two minutes per question, with a few minutes at the end to enter answers onto the answer sheet and quickly check everything is in order. Many candidates actually fail simply as they do not allow enough time at the end for this basic task. You have to be ready to work fast!
4. Make or Break
No matter how good your resume is, if you fail the PST McKinsey will not consider you any further and you will not be invited to interview. Remember, there will be hundreds of candidates with comparable resumes and the Problem Solving Test is given precisely to thin down this field. Passing is mandatory. Even after you pass and interview, your PST score will be considered alongside your interview performance to determine whether you are given an offer.
5. 70% Cut-Off
Success in the PST is an absolute function of your score rather than how it compares relative to other candidates - there is no "curve". As such, performing better than the next candidate will be meaningless in itself. If all the candidates are sub-standard, all will fail.
Whilst McKinsey does not publish the exact cutoff for the PST, the best estimates (based on surveys of successful candidates) place it at around 70%.
One important point to remember is that you should give an answer for every question even if you are not entirely sure. The PST is not scored negatively - that is, for the PST McKinsey will not penalise for incorrect guesses (as per the system many medical students will be familiar with). As such, you should always give your best guess, just in case you get lucky.
6. 1-in-3 Success Rate
Whilst scoring is absolute, unofficial surveys have indicated that a fairly regular PST pass rate at around 33%. Most of those candidates who fail do so because they didn't work efficiently enough and/or failed to manage their time correctly, rather than because they lacked any cognitive capacity. One of the major causes of failure is actually candidates not allocating sufficient time at the end of the test to fill in the PST answer sheet!
The takeaway here is that the McKinsey Problem Solving Test should be treated more as a skill-test to be practiced for, rather than as some assessment of raw intelligence you can simply walk in and expect to pass if you are clever enough. You need to understand the relevant time saving methods and strategies to approach the test as a whole if you want to pass and eventually land your job at McKinsey.
7. McKinsey PST vs GMAT
If you have never sat the GMAT, you can skip this point. Many candidates who have previously prepped for and sat the GMAT suffer from a false assumption that the PST will be the same test by a different name - that there are very few diffences in the McKinsey PST vs GMAT. However, despite the similar format, this is not the case.
There is some overlap - for instance, you will need to have strong math for both. However, the PST requires a totally different, less academic style of math, where you need to be able to estimate, prioritise calculations and know how to take the right shortcuts (our mental math article is relevant on the differences here). Generally, the PST and GMAT serve different purposes and are tailored to those purposes in different ways. As such, you need to treat the PST as its own beast and prep for it accordingly.
An AI-based, bespoke preparation plan
We’re all trying to get to the same place, but from different starting points. MCC automatically tailors your preparation to your own specific needs. Get startedSix Question Types
As we have noted, the McKinsey PST is partitioned into three business cases, with eight to ten questions for each case. As with a real project, or indeed a case interview, you will be presented with data in charts or tables as well as with descriptive text. Typically, each individual piece of information will be followed by two to three questions referring to that information specifically.
PST questions can be split into six groups which can be expected to account for different fractions of the test. Let's take an in-depth look at each:

1. ~35% - Reading Facts
Reading facts PST questions test your ability to extract and elaborate data from graphs and tables. These are the most common question type, and you can expect them to make up around 35% of your PST.
Typical Formats
- Which of the following values is the best estimate of ...?
- Which of the following statements is valid, based on the data ...?
- What is the current ranking of options 1 to 5?
Examples
- Which of the following values is the best estimate of ABC revenue in Year 4?
- To the nearest tenth percentage point, what is the difference between Italy’s and Spain’s respective average annual agriculture sector growths due to fertilizing over the last 10 years?
Worked Example
The table below shows the sales development of the Topstar business unit across the main markets.
| US$ M | 2008 | 2009 | 2010 | 2011 | 2012 |
|---|---|---|---|---|---|
| US | 240 | 282 | 343 | 405 | 469 |
| Germany | 144 | 165 | 186 | 204 | 237 |
| Italy | 45 | 58 | 58 | 75 | 82 |
| China | 60 | 69 | 67 | 71 | 74 |
| Japan | 58 | 50 | 50 | 56 | 58 |
Which of these markets showed the fastest sales development (in percentage terms) from 2009-2012?
- US
- Germany
- Italy
- Japan
Method
As you can see, two minutes is not a lot of time to solve this! Let's have a look at an efficient method to let you get to the answer as quickly as possible. The steps identified here generalise to other reading facts questions.
-
Read the question - pretty straightforward in this case, as you are asked to identify the country with the highest growth rate.
-
Read the answers - there are four countries to be compared.
-
Go back to the table - compare the growth rate, between only 2009 and 2012, for those four countries. Simplify figures as much as possible and run precise calculations only if you find out that the difference between two countries growth rates is not large enough to guarantee a reliable result through simplification.
-
Define the calculation - you need to work out the form of the equation you would need to solve in order to calculate market growth. This will be:
Now you can put the equation to work. Start with the first option - the US. Approximately, US growth will be:
From simple inspection, this is obviously much higher than 50% - it is around 70%.
You can then move on to other countries using this US value as a benchmark and comparing them solely to that value. Germany's growth will be:
This is very close to 50% - so obviously less that the ~70% of the US. You can cross out Germany as an incorrect answer. Note that, if the value for Germany had been higher than the US one, you would have crossed out the US and gone forward using the German growth value as your benchmark.
For Italy, the calculation will be:
1/3 is (roughly) 33%, so obviously lower than 50% and certainly lower than the US. Cross out Italy!
For Japan, growth was from 50 to 58, so there is no need to make any calculations in order to rule it out.
This leaves he US (option A) as the correct answer.
Tips and Tricks
There are a couple of tricks you can employ to get through Reading Facts questions more efficiently:
1. Begin with an end in mind
Before performing any calculations, be clear on which formula/equation you need to use. This is crucial as there is no time for trial and error in the PST. Spending just a few more seconds nailing down the exact formula you need at the beginning will pay dividends by saving you much more time in the calculation phase.
2. Minimise the number of calculations
When going through your solutions, you will be surprised by how many calculations can be avoided or approximated mentally. The fundamental question you should ask yourself before performing any calculation is "does this affect the answer?". This might sound a little odd, but it is a habit which you must form to become quick enough to pass the McKinsey PST. Here are a couple of examples where you can "work clever" to avoid redundant calculations:
The Anchoring Technique
This the technique we used in the example above. When looking for the highest value amongst several possible answers, run calculations for the first answer and use that value as a threshold value as you work through the others. If other answers look immediately wrong, do not perform any further calculations - just as we did with Japan, above. (Generally, you can almost think of this as a less probabilistic version of the solution to the secretary problem.)
The Selection Technique
Here, you pre-select only the calculations which are essential to identifying the answer. For example, the question below asks you to rank the effectiveness of 5 solutions:
- 1, 2, 4, 3, 5
- 1, 2, 3, 4, 5
- 1, 3, 2, 4, 5
- 1, 3, 2, 5, 4
Calculating whether solution A is the most effective is a complete waste of your time – it is the least answer-changing analysis. Instead, calculate which is the most effective between solutions B and C, working from there.
3. Master quick percentage calculations
Growth rates and percentages are ubiquitous in the McKinsey Problem Solving Test. In particular, it is pretty much a certainty that you will be asked to calculate growth rates over multiple time periods. This is theoretically feasible by hand, but extremely time-consuming. For example, say the revenues of a given company are growing at 5% per year for four years. In order to get a precise result, you would need to calculate the four year compound growth rate as follows:

Quite simply, regardless of how quick you are at math, you absolutely do not have the time to go through this whole calculation. It would almost certainly take more than two minutes just for this step, which might not actually be enough to answer the whole question (usually, calculating such a percentage will only be a subset of a question).
Instead, you can arrive at an approximate but good-enough value for this growth rate by using a straightforward shortcut. To do this, we simply multiply the growth rate by the number of years it will apply for, estimating the compound growth rate. Here, this will be 5% x 4 years = 20%.
There are a couple of caveats here which will already be obvious to more mathematically inclined readers:
- With positive growth rates, the compound rate will be underestimated. Above, we estimate 20%, but the real figure is actually 21%. Conversely, with negative growth rates, this method will overestimate the compound value.
- The greater the magnitude of the annual growth rate and the greater the number of years for which it is applied, the less precise this technique becomes. For instance, five years of compound growth at 5% per annum yields a 27% compound growth rate, whilst this shortcut would give us a value of 25%.

2. ~18% - Root-Cause Reasons
Root-Cause Reason PST questions test your ability to identify the causes underlying business problems. These questions begin from some fact about a business, which must be explained. The candidate is then given a list of putative explanations for this fact. However, only one of this list of suggestions is actually a logically valid explanation of the phenomenon in question. The candidate must identify which this is.
Examples
- Which of the following reasons, if TRUE, is most likely to be the reason for the drop in house prices in year two?
- Which of the following, if true, LEAST explains the data for Slovenia and the Czech Republic in Exhibit 2?
Typical Formats
- Which of the following reasons, if TRUE, best explains the reason why the CEO wants to proceed to ...?
- Which of the following does NOT help to explain why ...?
- Which of the following, if TRUE, would best challenge the sales manager's decision?
Worked Example
Zapclothing is a global fashion retailer, traditionally catering primarily to teenage girls and with shops across Europe. Five years ago, the senior management at Zapclothing decided to embark up an move upmarket, with the aim of catering to a slightly older and more affluent customer base.
Leading French and Italian designers were hired to create unique and exclusive lines for Zapclothing, whilst prices were raised across the entire product line by 20-30%. A series of events were held in all major global cities in order to launch the new incarnation of Zapclothing as a brand with a more sophisticated, upscale image.
Initially, this mid-market transition boosted profit margins without altering sales volumes. However, one year later, the company has found itself with plummeting revenues and a decreased profit margin. In order to return profits to their previous higher levels, the marketing manager has proposed a permanent price reduction of 10% across all lines.
Which of the following facts, if true, would best challenge the sales manager's price reduction proposal?
- Over the last year, due to higher commodity costs, prices increased by 15% on average for the whole fashion industry
- Consumers consistently quoted price among the top three quality attributes for mid and high-level fashion brands in surveys over the last 5 years
- In a recent survey, over 80% of the existing customer base claimed that they would still buy more than 50% of their clothes from Zapclothing, regardless of price
- Females aged 20-30 consider price among the top three criteria for deciding whether to make a purchase
Method
- Read the question carefully, making sure that you understand what is being asked.
- Scan the answers and underline the key words in the text. Don't spend any more than 10 seconds on this step - the intention is simply to make you quicker in finding the relevant parts of the introductory paragraph.
- Think carefully about how this proposal can be challenged. The most effective challenge is necessarily that acting based on this proposal would not help to solve the company's problems - in our example, restoring high revenues. If this is the case, then the proposal does not correctly identify the cause of the focal issue.
- Go back to the answers, crossing out the incorrect ones. Let's see how we assess the four answers in our example:
- Not relevant. The fact that prices increases increased on average by 15% for the whole industry does not tell us whether a decision to reduce prices would bring in additional revenue from existing and/or new customers. FALSE
- If consumers consider a higher price to be a signal for superior for mid and high-level fashion brands (where Zapclothing hs positioned itself), reducing prices could have a neutral or even counterproductive effect on revenue growth. TRUE
- Not relevant. This statement is only relevant to revenue derived from existing customers. Even if the behaviour of current customers was entirely unchanged, revenues could still be grown by tapping the pool of potential new customers. The information provided is incomplete and would not be sufficient to challenge the sales manager's proposal. FALSE
- Opposite Direction. This fact would not challenge the sales manager's idea, but reinforce it. FALSE
Practice makes perfect
Get startedTips and Tricks
Correct answers in Root-Cause Reason questions will always have two elements in common:
- Relevance - they have a significant effect on the target stated in the introductory paragraph
- Correct Directionality - their effect on the target should be going in the direction required by the question
As we have already observed in the example above, there are generally three kinds of answer in Root Cause Reasons:
1. Not Relevant
These are answers which have no, or only limited, effect on the proposal in question (as with answers A and C in the example above). By identifying the kind of fact which would have some bearing on the proposal, you will be able to quickly pick out answers which simply have no influence on the relevant issue.
Note here that you should always be careful not to assume anything which is not explicitly stated. Often, there can be a temptation to think beyond what is actually on the page. For example, when you are assessing C above, some candidates might assume that the preferences of existing customers will also be representative of potential new customers as well, or perhaps that the focus on existing customers indicates their particular importance to the problem. This would make C seem more relevant to the sales manager's proposal and would thus then ultimately lead you into error. PST questions are a test of your ability to read closely and think logically - not of your imagination!
2. Relevant, But With the Wrong Directionality
These answers affect the proposal in question, but with the effect going in the opposite direction to what you are looking for. For example, D above actually reinforces the sales manager's proposal rather than challenging it.
One of the most common errors in Root-Cause Reason questions is selecting answers which are relevant, but with the opposite directionality to what the questions is asking for. As such, you must always keep in mind what the question has actually requested and the kind of answer which fulfils that request.
3. Relevant and With the Correct Directionality
These are answers which significantly affect the proposal in the correct direction, according to the parameters set by the question.
3. ~17% - Fact-Based Conclusions
Fact-Based Conclusion PST questions test your ability to draw logical conclusions from a collection of facts. These questions can manifest the greatest degree of variation of all types, and can range from something relatively similar to a Reading Facts question to a requirement for you to make some very tough inferences from rather vague introductory text.
Typical Formats
- Which of the following statements can be concluded from ...?
- Based on the data on table ..., which of the following statements is a valid conclusion?
Worked Example
Pharcom is a global pharmaceutical company engaged in the development of small molecule drugs. Your team has been called by the Head of R&D to help him pre-select the drugs that are most likely to reach patenting and commercialization. He claims that, on average, 12% of researched drugs are cleared to be marketed, while the remainder are dismissed either during the R&D process or at final certification. Currently the average total expense for every drug in development is £12m and the full trial and certification lasts for 10 years for the drugs going through the full process. The research and development process of the drugs is constituted by the following steps:
- Trial 1: Laboratory trial to test the effect of the active ingredients. The trial costs £3.5m and lasts for 2 years.
- Trial 2: Laboratory trial to test the impact of side effects. The trial costs £4m and lasts for 1.5 years.
- Trial 3: Animal testing to evaluate bacteria resistance. The trial costs £4.5m and lasts for 4.5 years.
- Final certification by Food and Drug Administration. Filing costs £4.5m. Certification lasts for 2.5 years.
Which of the following statements can be concluded based on the information above?
- Most drugs complete the entire research, development and certification process.
- Before being either approved or dismissed, drugs remain in the development and certification process for an average of 7.5 years.
- Reducing by 50% the length of Trial 2 and Trial 3 would reduce the total cost of the Pharcom research and development process by £4.25m.
- Over 50% of the drugs reach Trial 3 stage in the research and development process.
Method
- Read the question carefully and make sure you understand what is being asked.
- Read the answers and underline key words in the introductory text. Identify the specific graph or portion of the introductory paragraph each answer refers to.
- Start with the numerical answers. These are often the clearest and most straightforward to solve. Generally, go back and forth between the answers and the introductory text and any figures. To identify the correct answers, it helps to consider whether the opposite of the statement would be true.
-
Go back to the answers, crossing out the wrong ones:
- Since the average cost per drug is £12m, we can quickly establish that the average time in the pipeline is 8 years - at the end of Trial 3 - as this is the point where £12m of expenses have been accrued (£3.5m from Trail 1, £1.5m from Trial 2 and £4.5m from Trial 3). Let's take the hypothetical case where 50% of drugs stay in the pipeline for 7.5 years and 50% for 8.5 years. In this case, no drugs at all complete the pipeline, but the mean time spent in that pipeline would be 8 years. Since cases where no drugs at all are approved are compatible with the information we have been given, we certainly can't safely infer that most drugs are approved. As such, we can rule out A. FALSE
-
As we have just established, the average time drugs are in the process before being dismissed or certified is 8 years (as the average cost of £12m is accrued by the end of Trial 3). Obviously, then, the value here of 7.5 years in wrong. FALSE
-
We simply don't have the information which would be required to know if this statement is true or not. It might be tempting to imagine here that if we halve the time for a trial, we halve the duration of a trial, then we halve its cost - this would indeed yield a value of £4.25m. However, we have no justification for the assumption here that cost varies with time in a purely linear fashion. In more usual business terminology, we cannot assume that the costs associated with trials are purely variable, so that halving the trial's magnitude halves costs. There might be fixed costs which are incurred regardless of trial length - perhaps administrative costs in setting up the trial or the cost of buying equipment, recruiting staff etc. Clearly we cannot state C to be true based on the information we have. FALSE
-
Trial 3 is reached after 3.5 years - that is, the total duration of Trials 1 and 2. As above, the average time each drug spends in the pipeline is 8 years. Now, mathematically, it is entirely possible for mean and modal values to diverge significantly. This is to say, it is possible for more than half of drugs to be in the pipeline for much less than our 8 year average value as long as there are some drugs staying in the pipleline for much longer so as to balance them out.
Let's take another hypothetical extreme case. We could keep a mean of 8 years but approach the case where the majority of drugs did not make it to Trial 3 by assuming that 50% of drugs are rejected just slightly before the 3.5 year mark. To keep a mean of 8 years, then, the other 50% of drugs would need to remain in the pipleine for 12.5 years. However, the maximum length of the process before certification is 10 years. As such, we know that more than 50% of drugs must be in the pipeline for more than 3.5 years - and thus make it into Trial 3. TRUE
Tips and Tricks
In dealing with Fact-Based Conclusion PST questions, there are three types of answer which you might encounter:
1. False Conclusions
Some answers might simply be false or wrong. Even if they seem logically sound, the outcome might be reversed or otherwise wrong.
2. True Conclusions
Answers which both have sound logic and draw the correct conclusion.
3. Unproven Conclusions
The logic here might be correct and the conclusion might well seem reasonable. However, they cannot be fully supported by the facts which have been presented to you in the introductory text and/or graph.
How to discern false answers from true ones
Telling apart true and false answers can be both challenging and time consuming. In particular, some answers will require to mentally estimate a whole set of values for which statements or relationships might hold. Here are two steps which might prove useful in assessing a statement:
Can the opposite also be true?
Always consider whether the opposite of what has been stated can actually be disputed. Candidates typically fail to ask themselves this question, but it can be highly revealing. You will be surprised at how much of a difference asking this simple question can make.
Consider the extremes
Answers should always hold true - not just most of the time. If an answer is not always true, it is not valid. A variant of this method we used above to verify answer D above - we considered the extreme values which would could notionally maintain the average of 8 years, but then ruled these out as impossible within the bounds of the question.

4. ~15% - Word Problems
Word Problem PST questions require you to solve business problems by combining information across sources. In other kinds of question in the Problem Solving Test, you will find all the relevant data from exhibits or introductory paragraphs. However, in Word Problems, part of the challenge is that the relevant data is spread between the question itself as well as the introductory text or exhibits. If you have taken the GMAT, you will find that word problems are the closest of the PST question types to what you will find in the GMAT.
Examples
- Assuming that a machine costs $2m, how many years will it take for the firm to break even from its investment?
- If an average employee is paid 12 hours per month, which of the following formulae accurately calculates the average number of items handled per employee, per month?
Typical Formats
- If employees’ salaries are increased by 20%, what is the increase in productivity required to break even?
- Assuming that the economy keeps on growing at 2% per year for the upcoming 10 years, which of the following equations best approximates the decrease in the debt/GDP ratio?
Worked Example
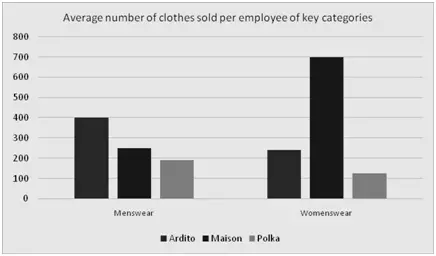
Ardito, a leading fast fashion retailer, has 79,000 employees spread over 3,350 branches. Maison operates on approximately 25 FTE employees per retail branch. Approximately, how many more branches than Ardito should Maison have to sell as many items in menswear as Ardito?
- 500
- 1,700
- 5,000
- 127,000
Method
- Carefully read and understand the Word Problem
- Go through the answers to assess the level of precision which you are going to need in your calculations. Here, since the answers are quite far apart, you will be able to estimate rather than calculated precisely.
-
Build your equation:
First, consider what has to be kept constant
Hence, if we assign the variable
as the number of additional branches Maison requires in order to sell as many clothes as Ardito:
This yields:
At this point, we have two possible solutions. The first is as follows:
The final answer will be between 1000 and 2000. Thus, we know the answer is B. However, note how many steps and how many calculations were involved here - you almost certainly won't be able to get this done in under two minutes!
The second solution takes care of this problem and is as follows:
Here, you simply plug numbers from the answer options into the equation and see which would make that equation work. This method is by far the more efficient way to solve this kind of problem.
Quickly, we can see that 1,700 is the only result fitting the equation. Thus, the answer is B. Note how much faster this was than the first solution.

5. ~10% - Client Interpretation
Client Interpretation questions focus on understanding project requirements and the analyses which will be necessary to tackle the client's concerns. In consulting projects, you will engage every day with various stakeholders from the client company . Fundamentally, client interpretation questions are about understanding:
- What the client says that can have an impact on defining the scope of your project
- What the client implies about given choice or strategy
- Which are the best analysis decisions to take in order to fit the client’s needs
Typical Formats
- Which of the following best summarizes the CEO’s concerns?
- Which of the following statements best describes the thoughts of the CEO regarding...?
- Based on the opinion of the Head of Department, which of the following statements is/are valid?
- Which of the following statements best describes the CEO’s aims for the McKinsey study?
- Which of the following analyses would be LEAST useful to address the CEO’s concerns?
- Given the aims of the CEO, what would be the LEAST relevant question for the team to answer?
Worked Example
Soul is a leading fashion retailer, selling clothing, shoes, make-up and accessories. It has around 400 shops worldwide, of which 200 are in the UK. Soul operates through a franchising model, where shops are run by private independent companies who pay a royalty fee to Soul. In exchange, Soul designs the shops and supplies them with new clothing lines, manages branding and advertising, sets promotions and provides shop-owners with guidance on all standard operating procedures for running the shops. This strategy enabled Soul to dramatically grow in scale, boosting shop opening and customer base. However, customer numbers have recently plateaued, resulting in slower sales and profit growth.
The CEO of Soul has engaged your team to help understand whether the recent changes in revenue and profitability trends are related to unsatisfactory shopping experience. He is convinced that the recent growth in scale came at the expense of a consistent shopping experience across all locations. He tells the team “I am sure that the responsibility of the current slowdown lies in poor delivery by the shop owners. I recently visited five shops in different countries and three of them did not fully apply our policies ensuring consistency in shop layout and pricing policies. This is disorienting our customers and pushing them to seek out our increasingly aggressive competitors”.
Which one of the following answers BEST describes why the CEO has engaged your team?
- He wants help in implementing a coherent and consistent brand image and shopping experience across all shops.
- He wants to identify the causes of the inconsistent shopping experience across shops in different countries.
- He wants to validate his hypothesis that an inconsistent shopping experience in different stores led to declining revenues and profitability.
- He wants to overhaul the set of policies and standard operating procedures imposed to shops in order to guarantee a consistent shopping experience.
Method
Here, two aspect of the established method from above take on increased significance over the others:
- Read the question. This is generally pretty straightforward, and simply enquires as to the client's reason for engaging McKinsey.
- Scan the answers and underline key words. Do not spend any more than 10 seconds on this step. As before, the purpose is simply to facilitate finding relevant pieces of information later.
- Go back to the text and quickly jump to the relevant part. More than 50% if the paragraph is of little or no use. Precisely reading the essential sentence will be enough to answer the question.
-
Go back to the answers, crossing out the incorrect ones:
- This answer may be true, but it does not capture the purpose behind engaging your team. The CEO did not call your team to advise him on branding or design, but because he wants to understand the causes of his company's downturn. FALSE
- The reason for engaging your team is not to understand the causes of the poor shopping experience, but the causes of the downturn - these are not necessarily going to be the same thing. FALSE
- The purpose of this engagement is finding out whether inconsistent shopping experiences across stores led to the current downturn. TRUE
- Again, this answer could be true, but it is not the reason for engaging your team. The CEO did not bring you in to redesign policies, but to understand the causes of the downturn. FALSE
Tips and Tricks
- Highlight the keywords in all answers. Prioritising the right words and sentences will save you a great deal of time.
- Cross out incorrect answers. Often, one or more answers will be clearly incorrect, whilst two or more will appear to be correct or almost correct. Cross out the obviously wrong answers before returning to the introductory text to pick out which of the "almost right" answers is actually correct.
- Beware of the "sensible answer trap". Sometimes, answers contain implications which look rational and sensible. However, be very careful about making assumptions beyond the information you have been supplied. No matter how reasonable a statement might seem, if the client has not actually said something to that effect, that statement is simply not valid.

6. ~5% - Formulae
Formulae PST questions ask you to express a quantitative word problem as a symbolic formula. This will test you capacity for abstraction by challenging your abilities to extrapolate from data, break down problems and identify drivers and directions of causality.
Example
Which of the following formulae calculates the share of non-performing loans out of total loans?
Typical format
Which of the following formulae best approximates ...?
Worked Example
Forman Fisheries is engaged in packaging shrimp and other fish. Shrimp are graded from A to D depending upon their size and taste. Below are some key productivity indicators for Forman Fisheries' shrimp packaging activities:
| 2012 | |
|---|---|
| Grade A shrimps packed in a month (a) | 3,600 |
| Grade A shrimps share of total shrimps (b) | 12% |
| Total boxes per year (c) | 8,900 |
Assuming that all boxes contain the same quantity of shrimps, which of the following formulae best approximates how many boxes of non-grade A shrimps were packed in the last month?
Method
- Homogenise your units of measurement. Since we are looking at a number over one month, wherever we will need the quantity of total boxes c, we will divide it 12, since it is an annual indicator.
-
Break down the problem into smaller steps. This should help you get to the relevant ratio more quickly. In this case:
Identify how to solve for each of the elements of this equation:
Therefore:
Simplifying:
And thus the correct answer is answer D.
All you need to pass the McKinsey PST
Learn moreTips and Tricks
Sometimes, answer formulae are presented with various simplifications which can make it time consuming to figure out whether they are correct. However, formula questions are about extrapolating a formula which should work with any value for each variable.
A trick to double check your results is to replace some of the values in the table with simpler ones, come up with a solution and then plugging these simple values into the formulae to see if they produce that same solution.
For example, in this case, assume that:
Grade A shrimp share of total shrimp (b) = 10%
Total boxes per year (c) = 1200
Therefore, boxes per month = c / 12 = 100 per month
Since all boxes are the same size, non-grade A boxes will be:

Now that you know that a correct equation will generate a result of 9, you can plug the numbers above into each of the options and check which produces 9 as an answer. This trick works especially well when the formulae involve high degrees of simplification.

Skills Tested
Each PST question type tests a subset of the skills that are useful in consulting. It is worth remembering that there is only so far practicing PST example questions alone will get you if you have not taken the time to develop these skills. Think about a kid trying to learn math - they can spend hours looking at all the sums they want, but they won't get very far if they haven't learnt to add yet!
Since these are the exact same skills that are assessed in your case interview and via your resume and cover letter, it makes sense to learn exactly what they are and what is required of you. It is worth noting that this is the same overall consulting skillset is the same one we teach in our Case Academy - our approach is consistent across the whole recruiting process.
So, what are these skills?
-
Identifying Root Causes
Just like doctors, consultants focus on identifying and treating the underlying causes of a problem. When you address a problem, you shouldn't ever stop at the superficial level of observable symptoms, but must dig deeper and find the real issue underlying what you are dealing with.
For example, imagine a doctor who has a patient complaining of persistent headaches. A good doctor is not just going to keep dishing out painkillers, but are going to want to establish what is causing the pain. It might be, say, that the headaches are caused by poor eyesight. If so, the patient will be dispatched to the optician to get some glasses to solve the problem more permanently.
-
Draw Fact-Based Conclusions
Consultants always anchor their diagnoses and recommendations on data and analysis - never on opinions or hunches! This is called a fact-based approach.
-
Prioritisation
In order to be able to correctly answer all the PST questions (and fill in that answer sheet!) within the time limit, you will need to be able to prioritise important data and calculations, effectively deal with uncertainly and generally find a good compromise between accuracy and speed. This includes the ability to select salient information from large volumes of text and to deal with ambiguity within that text. Once they are on top of the raw facts of what is happening, consultants will always then extract the salient implications - or the "so-what" - of the situation, rather than just re-describing the same data.
-
Numerical Agility
Most PST questions will require you to perform some kind of calculation. Since you are not permitted to use a calculator or similar, you are going to have to be very comfortable with mental math. In particular, you will have to be able to make estimates very quickly. We have an article on mental math for consulting, as well as a free practice tool, which will be a great starting point to sharpening up your skills and learning the various shortcuts to make your calculations faster.
-
Reading Charts
To pass the McKinsey PST as well as to get through your case interview, you are going to need to be able to quickly and reliably infer relevant information from complex graphs and tables. This information will be used to find root causes, draw fact-based conclusions or as the starting point for mental math problems.
-
Set-Up and Manipulate Formulae
The McKinsey PST doesn't require super-complex math, and certainly nothing beyond high school level. McKinsey PST formulas will always be realtively simple ones and you will not have to muster any complex algebra. However, what will be different from a high school math question is that it will be much less clear as to how you should be approaching problems. You will often have to set up equations by extracting one or two salient relationships from a large amount of otherwise irrelevant information. Identifying what is relevant will be the real challenge rather than the relatively simple math. Subsequently manipulating these formulae will come relatively easily to many of you. However, the time constraints and lack of a calculator in the PST will necessitate even the most mathematically gifted to be somewhat strategic in terms of how they chose to solve problems. You will need to avoid analyses that will take too long and which you cannot complete without a calculating aid.
Each of the skills above will be tested in different kinds of question. Be sure to keep a note of which skill in particular has let you down each time you have a problem with a PST question. After a few questions, you should have an idea of where your systematic weak points are and thus where you should focus your efforts to improve via building stronger skills. If your mental math is constantly an issue, go to our mental math article. If you are struggling with identifying root causes, our article on identifying the problem in case studies would be a great place to start.
The important point is that you won't get really good at PST questions simply by doing PST questions - you need to build the right skills! It is worth noting here that our Case Academy teaches precisely the consulting skillset as the McKinsey PST requires (usually case prep systems just teach question-specific frameworks, but we focus on fundamental skills). As such, working through the Academy will not just prep you for case interviews, but also build the full skillset required for the PST. If you are intent on going all the way through the selection process with McKinsey math prep and other aspects of skill building only need to be done once. Two birds with one stone - an efficient use of time!

Optimal PST Prep: Plan and Test Strategy
By now, you will have a good idea of what the McKinsey Problem Solving Test is, what the questions look like and the skills it is assessing. The categorisation of different question types and the methods and tips we have discussed for each already give you the building blocks for a solid prep. However, to make your preparation both as effective and time efficient as possible, you should really begin by making a plan to provide some structure. This will make sure that you don't miss out any key elements and also that you distribute your time sensibly.
As you will have realised by now, the PST is difficult - especially because of the acute time constraints. Having made a plan and diligently practiced all your skills might not actually be enough to pass. You also need to consider your strategy for tackling the test optimally. We have already given a few tips on this, peppered throughout the sections above, but there are also several points on general test management which you will need to know about.
Let's look in more depth both at how you should plan your prep and at your strategy for approaching the McKinsey Problem Solving Test:
Preparation plan
Don't be fooled by those who repeat the old mantra "practice, practice, practice". While practicing is very useful, relying entirely on "brute force" practice with PST sample questions can be remarkably ineffective and a way to set yourself up for failure.
A more sophisticated, more effective prep plan will be made up of the following elements:
1. Skill Building
You need to build your general consulting skillset to be able to reliably perform well on real PST questions. This will never be wasted time, as you will need exactly the same skills in your case interview - and indeed for when you (hopefully) start the job! In particular, given nobody will be starting entirely from scratch on these skills, you need to identify and work on your areas for improvement. As mentioned above, you should take note of where you are underperforming and address your attention there. In particular, you will want to focus on the following:
-
Numerical Agility
Being able to perform mental math quickly is arguably the single most essential skill required to pass the McKinsey Problem Solving Test. In particular, you will find that the need to make rapid estimates will recur constantly in PST questions. This includes understanding the appropriate degree of approximation as well as getting through calculations quickly. The mental math video in the Efficiency Tools section of the MCC Academy will provide you with all the fundamentals and all the tricks and methods you need to be genuinely quick with numbers and is a great way to get to grips with everything quickly and without missing anything out.
-
Reading Charts and Solving Problems
Again, the ability to extract information from diagrams and set up and solve mathematical problems are critical to being able to deal with many PST problems. Indeed, the numbers and equations for your mental math must come from somewhere! You will have to read charts in the McKinsey PST and will have to do so under severe time pressure. Similarly, various types of PST question will test your ability to work through problems in an efficient fashion. Our mental math article deals with reading charts. We also cover this whole area in great detail in the MCC Academy course and also include extensive drills in our Beyond Test Ready package.
-
Identify root causes and draw fact-based conclusions:
Being able to wade through information and identify fundamental causal drivers and synthesise findings into takeaways fully supported by the data are key consulting skills and one which your PST will test across multiple questions. To help you prepare as thoroughly as possible for these, we provide 10 specific sample questions on these areas in each of our Test Ready and Beyond Test Ready packages.
2. Refining
To optimise your performance on the PST, your prep should always include a blend of practice and skill building. Your first step should be to try a practice PST to see where exactly your weak spots are. You should then work on these particular skills using other resources, (such as the articles on this site and the lessons in MCC Academy). You can then return to another practice PST to see how you have progressed and where you should then focus on your next bout of skill building. You should then iterate this process until you are ready to take the PST for real.
It is worth noting that this method also makes sense at a more pragmatic level, as there is only a limited supply of sample PST test papers available to practice with online. This iterative approach, then, has the added benefit of letting you make best possible use of the scarce resource that is PST examples. The skill-specific questions provided in our Beyond Test Ready package also help deal with this lack of practice material and are invaluable in the skill building process.
3. Simulation
Once you have practiced enough, it will be time to step up to simulating the real PST more fully. There is a temptation to skip what might seem like the "theatrics" of a full simulation. However, you cannot just assume that it will all be fine on the day! This is the same rationale for why your high school most likely had you sit full mock exams before important assessments, rather than just rely on class tests etc.
You should replicate the PST test environment as closely as possible. Print out your sample PST test paper, staple it and print out your answer sheet. Find a quiet room and do the test strictly in the allotted time and without a calculator or any other such "contraband". You might feel a bit silly doing all of this, but it really is worth it. Sticking exactly to the rules is the only way to really practice your PST test strategy. Even relatively small things like becoming accustomed to keeping your notes entirely in the booklet and actually filling in the answer sheet at the end will save you precious time in the real PST.
4. Keeping an Error Log
When you run through a practice test with a mark scheme, everything will seem very easy. "Oh, of course, that's exactly what I should have done..." Fast-forward couple of weeks later, though, and you will find yourself staring at a PST question with precisely the same structure, but with no idea of how to solve it.
This is precisely why you need to keep an error log. You might already be familiar with error logs from GMAT prep, but we recommend you extend the practice here. For the uninitiated, an error log is a continuous method of analysing practice problems to identify WHY you answered them incorrectly. In your error log, you should be keeping track of your mistakes and of what you found hardest (even if you got there in the end). As well as using this information to inform where your energy is focussed in skill building, you should also be running through your log frequently to ingrain the lessons you have learnt and generally consolidate your technique.
There is no single correct format for your error log. Some will prefer very organised, detailed logs, whereas others will prefer a more old-fashioned paper record. Really, you should chose whichever method you personally find most convenient, as what is most important is that you actually make consistent use of the log over time.
Whichever way you chose to set out your error log, though, we recommend that each entry should contain the following information.
- Question type - as per our categorisation above.
- Reason why you found the question difficult - you might have taken too long to answer or not been able
- Question and answer choices - record what the question actually was
- Proposed solution - work out the method which you should ideally have used to solve the question - that is, whichever solution you find quickest and most effective given your own abilities.
- Key takeaways - what you should learn in order to answer this kind of question more efficiently. For example, you might need to learn how to simplify fractions more rapidly or to improve your quick reading skills.
The "key takeaways" in your error log are what will guide the direction of your prep for the next few days, before you test your abilities again in the iterative manner we described above.
Whilst error logs help to marry skill building and practice - just as any optimised PST prep absolutely must - in forming part of the iterative method we describe above, error logs also take on a more pragmatic function. Whilst the McKinsey problem solving test sample itself is excellent and we at MyConsultingCoach have invested significant time and money into creating and perfecting additional content, this still ultimately adds up to a finite amount of practice material. This unavoidable constraint means that you must work sensibly to squeeze the greatest amount of utility out of what is available.
The amount of practice you are able to do will always be the ultimate bottleneck in any PST prep. Experiencing different questions will both let you take the iterative process of identifying and working on problems areas further, but will also make you less likely to be surprised by something entirely new in the real PST. Access to extra practice material is thus a major driver of increased performance on test day and - ultimately - landing a job. You will find practice tests at the bottom of this page.
PST guide and practice test
Get startedTest Strategy
Most McKinsey PST questions are not actually all that conceptually demanding. The real difficulty derives from the extreme time constraint. As we noted above, given three hours with the same PST test paper, everyone would pass. In practice, then, the successful candidates - who go on to get interviews and jobs - might not actually be the most clever or able, but will often simply be those who have been able to manage their time most effectively.
Obviously, we have already explained a whole host of time saving methods for use in different kinds of questions above. Building up your skills will also help get through questions faster - improving your mental math in particular will see significant reductions in your time taken per question.
However, to pass you must also consider your time usage not just individual questions, but for the problems solving test as a whole. In this section, then, we will go over both an overall test time strategy and a consistent strategy to answer PST questions:
1. Test Time Strategy
PST question difficulty varies quite significantly. Some questions are really quite straightforward to the point of being "easy". Others are seemingly impossible. Unfortunately, you can't expect to get a paper with only the easy ones (if only, eh!), but will have a mix of different difficulties across your 26 questions.
To start to optimise your approach, you should combine this realisation as to varying question difficultly with the following two facts we alluded to near the beginning of this article:
- All questions are worth the same
- There is no penalty for wrong answers (there is no "negative marking")
Now (as we keep mentioning), you will need to leave at least five minutes at the end to fill in the answer sheet. Of the remaining time, you can allocate two minutes to each of your 26 questions (the maths geniuses amongst you will note that that leaves 3 minutes spare, but you can be assured that they will disappear whether you like it or not).
Given that all the questions are worth the same marks, you simply cannot allow yourself to become bogged down on one particularly tough PST question and leave yourself without time to answer two easy ones. To avoid this, you should keep track of how far through the test you are relative to how much time has elapsed - that is, make sure you are actually getting through questions at a rate of one every two minutes. For instance, if you are 10 minutes in, you should at least be just finishing question five.
If you realise that you've fallen behind because you are stuck on a very hard question, you should not devote more time to it. Simply circle that question and what seem like the two or three most likely answers from your analysis so far.
If you get to the end of the test and have some time left besides that required to fill in the answer sheet, you can go back and look at the question again. Often, coming back and looking with fresh eyes will break you out of an analytic rut. However, if you still simply can't make head nor tail of the question, or if you end up without any more time to devote to it, you should simply pick one of your circled likely-answers at random and put that down on the answer sheet.
Don't feel too bad about this - the PST cuttoff pass mark is around 70%, so you don't need to have gotten everything right. Who knows, your best guess might end up to be the right one anyway! Even if you picked an answer at random it has a 25% chance of being right. An educated guess should have somewhat better odds than that.
2. Question Strategy
We have already said quite a bit above about how you should approach individual kinds of question. However, we can also make some helpful remarks about how you should be approaching each question more generally.
The first fact to note is that whenever you first sit down to a practice test, you will realise that a minimum of 20% of your mistakes are simply due to mis-read questions. Indeed, a great deal of excellent candidates will fail their PST ultimately because they failed to read a critical number of questions properly. It seems absurd when one considers how accomplished the average McKinsey applicant is, that they are effectively let down by their literacy! However, it is true nonetheless and you can see why we so consistently instructed you to carefully read all the different kinds of questions as we ran through them!
One of the main things the McKinsey PST assesses is your ability to deal with "information overload". This happens when you are presented with large volumes of text and/or quantitative data, where only some of it is relevant to the question you have been asked and you must work out which.
This actually simulates a some of the real demands placed on McKinsey's consultants, who will be confronted with all the complexity of the client firm's operation as well as the market it operates in and how it relates to firms up and downstream in its value chain. From here, the consultant must work out which aspects of the operation - and thus which portions of information - are actually salient to the client's question.
How you should proceeds next depends upon whether you have to chose between qualitative or quantitative answers:
Qualitative
Here, you should pursue an iterative method of going back and forth between the questions and the text, eliminating (and then physically crossing out to prevent any future confusion) incorrect answers one-by-one. This is fundamentally a test of your linguistic reasoning, though we have provided various hints and helpful techniques for different kinds of question above. Of course, the most fundamental advice we can give is to read PST questions carefully, but you can also do things like considering what would be true if the exact opposite of the focal statement were true.
Quantitative
You have a couple of options when dealing with quantitative answers, depending upon the specific nature of the question you have been asked. As such, you can chose to do either of the following:
The "Conventional" approach
Here, you simply identify the relevant data and solve the problem directly. Run through all the calculations on paper and then see which of the multiple choice answers matches the solution you generate. This is how you are probably accustomed to tackling problems from your education and will also be the best way to approach many of the questions in your PST
Working "Backwards"
Often, though, you will not have enough time to work through all the calculations required to answer a particular question via the conventional approach. In such cases, you will need to take a more strategic approach. We can do this by effectively working backwards from the answers. This is not as strange a method as it might sound - you simply need to build a framework of the relevant calculation and plug in the suggested answers until you find one that works.
Using this method can save time on multiple counts as, usually once you have found an answer that works, you don't have to take the time out to work through the other options (of course, in an ideal world you would indeed work through the other answers as a means to check for any mistakes on your own part, but time is precious in the PST and "done is better than perfect").

Practice Material
Having read this far, you should be well equipped to start preparing to take the McKinsey Problem Solving Test. The first step is to take one or two practice PST test papers. This will let you get a feel for what the tests are actually like generally, but - crucially - will also allow you to start your prep off with an idea of which skills you need to work on, as per our iterative method above.
You can find everything you need on this website or on the McKinsey website. Specifically, here are some PST samples to get you started:
- MyConsultingCoach McKinsey PST (free)
- McKinsey PST A (by McKinsey)
- McKinsey PST B (by McKinsey)
- McKinsey PST C (by McKinsey)
- McKinsey PST 2011 version (by McKinsey)
- McKinsey PST 2001 version (by McKinsey)

The Next Level
Beyond the free Mckinsey PST practice test linked above, MyConsultingCoach offers fully comprehensive PST packages to take your PST prep to the next level. Of course, you might pass the PST on your own. However, as we have noted, the average candidate only has a 33% chance of passing.
For those using an MCC package, though, that PST pass rate jumps right up to 85%. Given that you must pass the PST to get an interview and be considered for a job, this is a potentially enormous driver of whether you will work for McKinsey or not - that is the overall offer rate.
Whilst this is a premium service and won't ever be for everyone, if you really have a consulting mindset, then you can appreciate that - given the substantively increased likelihood of entry into McKinsey - the investment is more than worth it when balanced even just against the additional pay earned in year one versus a second tier consultancy. This is before we even consider the differences across your whole career and the prestige difference for your resume even if you move into other industries later.
We also stand by our service to the point that, if you don't pass your PST, we will give you half of your money back!

Next steps
So, what are you waiting for? Start your prep today and take a step closer to that your dream job with McKinsey!
Following our advice and making use of MyConsultingCoach resources will give you your best chance of success in the PST. Assuming you pass your PST, then, you will have to prep for your interview. As you probably know already, interviews at McKinsey and consultancy firms in general are not like a "normal" interview. The most notable difference is that you will have to solve a case study. This is a business problem which simulates the kind of project a real life consultant would called in to deal with.
As well as a case study, each interview will also have a McKInsey PEI or "fit" component, where your interviewer tests your motivation to succeed as a consultant and establishes whether your character is a good fit for the company. This is closer to the format of more familiar interviews. However, many candidates are ruled out based on their performance in this section, as they either don't prepare for it at all, or treat it too much like a "normal" interview. The demands even in the fit section of a consulting interview are significantly more rigorous than for interviews elsewhere.
In practice, one of the main differences in interviews in consulting and on other industries is the amount of preparation that is required. If you thought McKinsey PST prep was demanding, that was unfortunately just the tip of the iceberg. The stiff competition for McKinsey and other consulting jobs means firms can demand a degree specific preparation from candidates which is not really equalled elsewhere.
This might all sound daunting (frankly, if it doesn't, it should...). Don't worry though - MyConsultingCoach has you covered! This website is packed with articles which will give you solid overview of all the various topics you will need to understand (you can start with our articles on the case and fit interview and work your way out from there) as well as guidance on how to approach your prep in general.
For a more in-depth experience, we have also developed MCC Academy - a fully comprehensive case interview course. MCC Academy teaches the same consulting skillset as you will need for the PST, but in much more depth and applied to the business of cracking case studies. Other case systems simply teach a few formulaic "frameworks", with methods to approach a few common question types. However, this risks leaving you high and dry when the interviewer (as they likely will) gives you a questions that differs from the kinds you have learnt. By focussing on fundamental skills and teaching you to tackle cases in the same way a working consultant would, MyConsultingCoach equips you to cope with whatever your interviewer throws at you. Beyond this, the Academy also includes a set of lessons on how to perform in the fit component of your interview.
If you are serious about consulting in general, it makes sense to start MCC Academy alongside your PST prep, as the shared skillset makes for significant synergy generally and you will be able to use the Academy lessons to brush up your skills for the PST in particular. You will also then have plenty of time for case interview prep and not have to pack it all in after the PST.
Good luck with your prep!
A level of preparation you won't find anywhere else
Reason #1: Beat the time pressure
We developed techniques for each of the six question types in the McKinsey PST that will help you save time and boost your score. From practice, practice, practice to smart practice.
Reason #2: Focus your efforts
Our Performance Radar helps you pinpoint the question types where you need more preparation, enabling you to tailor your training and track your progress. No more random practice.
Reason #3: stretch your potential
Our tests were developed by a team of ex-McKinsey consultants and are constantly reviewed to provide you with the most comprehensive toolkit to succeed. Unlike many resources on the internet, our tests are realistic in their format (26-questions long, like the real PST) and challenging in their content.
Take our test for free
We developed a sample, 10-questions free test. We suggest you print out the test and do it on paper to replicate the real test environment
“The Performance Radar changed the way I prepared for the McKinsey Problem Solving Test: I moved from a random 360-degrees practice to a structured preparation focused on the areas where I was weakest. And those same areas quickly became the ones where I was getting the highest scores.”
Our pst preparation programmes
30 days money back guarantee on pst material
- 3 full 26-questions PSTs (78 questions)
- Performance Radar
- PST Guide
- 30 days money back guarantee*
- Straight to your inbox
- 3 full 26-questions PSTs (78 questions)
- 6 sets of 10 PST questions by type (60 questions)
- PST Performance Radar
- PST Guide
- All Consulting Math Material
- 30 days money back guarantee*
- Straight to your inbox
- 3 full 26-questions PSTs (78 questions)
- 6 sets of 10 PST questions by type (60 questions)
- Performance Radar
- PST Guide
- 30 days money back guarantee*
- Straight to your inbox
- Full length, 26-questions PST
- Performance Radar
- 30 days money back guarantee*
- Straight to your inbox
- Full length, 26-questions PST
- Performance Radar
- 30 days money back guarantee*
- Straight to your inbox
- Full length, 26-questions PST
- Performance Radar
- 30 days money back guarantee*
- Straight to your inbox
Frequently asked questions
When you do not have much time left we suggest you to:
- Understand how the test is structured: many people fail the PST simply because they don't know it well. You can find all the details about the PST on our PST Guide. You may want to double check the total time, since most offices will give you 60 minutes but some others 70.
- Develop a solid answering technique: It is essential for you to acquire an answering technique allowing you to make the best use of the very limited time in the test. Our video and the PST Guide will help you a great deal.
- Practice smart: We advise you to try the official tests on the McKinsey website (Test A, Test B, and Test C). If you want to boost your chances our best pick is the Test Ready Package above. You will have the chance to practice on three 26-questions full-length sample PSTs. Then, our Performance Radar will help you identify your weaknesses by translating results in your performance across the 6 PST question types. The PST Guide will teach you useful methods on how to tackle each question type and the 60 additional questions will help you master a sound technique for each of them. In other words nothing will be left off the checklist!
P.S. Do check whether the first round of interviews is immediately after the PST or on a different day. In the former case, we strongly advice you to prepare for case interviews. The Beyond Test Ready package also includes 1 hour of case interviews with our Mentors.
Passing the PST is hard mainly because of the time constraint. If you had 2 hours, you could easily score more than 90% - but you only have 1 hour. It is therefore essential for you to be able to manage time. Please use the video that's on the page.
Sure. You can ALWAYS upgrade from a smaller to a more comprehensive package.
Upgrading is easy:
- Purchase the new package
- Email us at info@myconsultingcoach.com within 30 days – we’ll refund your original purchase within 24 hours.